
I really need an explanation on this concept. Or I just can't decide if the function is continuous or not continuous at this point because it is not in its definition domain.
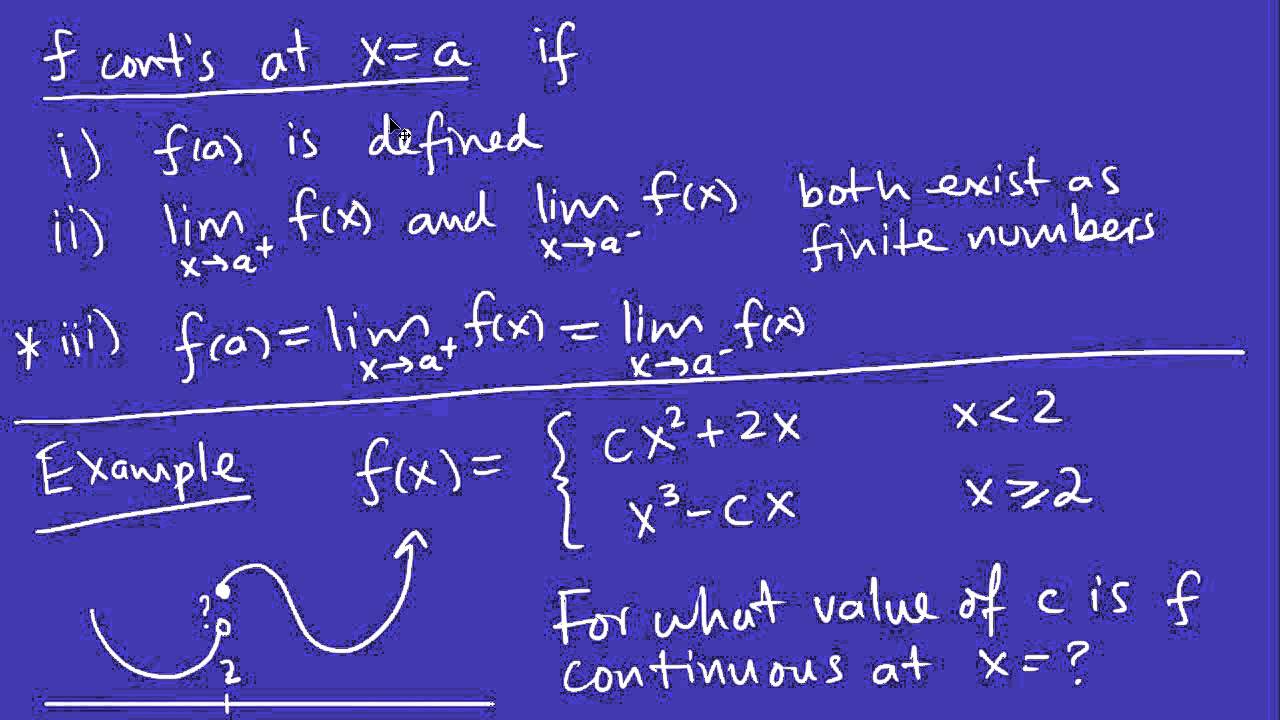
Obviously this point is not in the domain of this function, therefore, I do not know if the function has an asymptotic discontinuity at $x = \pi / 2$ A function is said to be discontinuous at a value a if there is a jump in the graph at a. Loosely and informally written, a function is continuous if there is no sudden jump in its graph, but rather the graph is connected. I'm right? Or should I say that the function has an asymptotic discontinuity at this point? why?Īs another example, suppose we want to study the continuity of the function $f (x) = \tan x$ at $x = \pi / 2$. In calculus, we typically assume that the functions we work with are continuous. Clearly the domain of this function is the set $(- \infty, -3) \cup (1, \infty)$, so, based on the above, since $-3$ does not belong to the domain of this function, I could say that it does not you can decide whether the function is continuous or not continuous at $x = -3$. At zero, since it is not in the domain, we cannot talk about whether it is continuous or whether it is not." Suppose now that we are asked to study the continuity of the function $f (x) = \ln (2x^2 + 4x -6)$ at $x = -3$. For example, the function $f(x) = 1 / x$ is continuous at all points in its domain.
#CONTINUITY CALCULUS HOW TO#
We learn how to find continuities graphically and through algebra in a step-by-step fashion. "It makes no sense to talk about whether or not a function is continuous at a point that does not belong to its domain. A function f is continuous at a point a if the limit as x approaches a is equal to f (a). I'm studying the concept of continuity and discontinuity of a function. Taking into consideration all the information gathered from the examples of continuous and discontinuous functions shown above, we define a continuous functions as follows:įunction f is continuous at a point a if the following conditions are satisfied.I'm confused with a fundamental concept of calculus about continuity. The limits of the function at x = 3 does does not exist since to the left and to the right of 3 the function either increases or decreases indefinitely. The function must be defined at that point, and The limit and the function must have equal.

The limits of the function at x = 2 exists but it is not equal to the value of the function at x = 2. Definition of Continuity The limit must exist at that point. The function is said to be discontinuous. Now that we can identify continuous functions, jump discontinuities, and removable discontinuities, we will look at more complex functions to find. In the graphs below, the limits of the function to the left and to the right are not equal and therefore the limit at x = 3 does not exist. Introduction to Calculus 12.1 Finding Limits: Numerical and Graphical Approaches 12.2 Finding Limits: Properties of Limits 12.3 Continuity 12.4 Derivatives. The graph has a hole at x = 2 and the function is said to be discontinuous. In the graphs below, the function is undefined at x = 2. These graphs have: breaks, gaps or points at which they are undefined. This lesson contains the following Essential Knowledge (EK) concepts for the AP Calculus course.


We now present examples of discontinuous functions. A little suffering is good for you.and it helps you learn. The functions whose graphs are shown below are said to be continuous since these graphs have no "breaks", "gaps" or "holes". We first start with graphs of several continuous functions. Introduction and Definition of Continuous Functions


 0 kommentar(er)
0 kommentar(er)
